Компилятор Fortran/C++ Intel 11
Примеры работы с компиляторами
- Компиляторы Intel Compilers 11 (C, C++, Fortran77/90, 95) используются на кластере по умолчанию. Команды: icc, ifort
- Информация для пользователей Суперкомпьютерного комплекса МГУ
- Сравнение опций оптимизации компиляторов Intel, GNU, PGI и PathScale на примере решения уравнения Пуассона
- Пример применения различных опций оптимизации
Рассмотрим задачу умножения 2 квадратных матриц 1000x1000.
Программа компилировалась с 5 различными флагами оптимизации:
- -O0 - без оптимизации
- -O1 - оптимизация для максимальной скорости, но без включения оптимизаций, которые увеличивают размер кода и при этом дают небольшой выигрыш по скорости
- -О2 - оптимизация для максимальной скорости (используется по умолчанию)
- -О3 - То же что и -O2, но включена более агрессивная оптимизация (в основном более агрессивная оптимизация для циклов), которая может не улучшать производительность для некоторых программ
- -fast - включает в себя -O3, а также ряд других флагов оптимизации, таких как -ipo (межпроцедурный анализ, замена вызовов небольших функций на их inline подстановки) и -xHOST (в случае процессоров Intel эта опция включает специальную оптимизацию для процессоров Intel с поддержкой SSE инструкций, в случае остальных процессоров код с поддержкой SSE инструкций для остальных архитекур).
Полученные результаты:
flags -O0 -O1 -O2 -O3 -fast Умножение матриц (сек.) 8.11 2.76 2.22 2.29 2.12 Использование базовой оптимизации в данном случае дает выигрыш по времени в 3.65 раза, что очень существенно. Однако, более агрессивная оптимизиция в этом же случае не дает выигрыша (-О3 и -fast).
Рассмотрим эту задачу на лучшем, по результатам первого запуска, ключе -fast с различными вариантами перестановок циклов. При этом память для матриц пусть выделяется по строкам:
double **a=(double**)malloc(sizeof(double*)*N); for (i=0;i<N;i++) a[i]=(double*)malloc(sizeof(double)*N);
Возможны 6 различных вариантов организации тройного цикла при перемножении матриц:
- первый цикл по i, второй по j, третий по k - кратко назовем ijk
- первый цикл по i, второй по k, третий по j - кратко назовем ikj
- первый цикл по j, второй по i, третий по k - кратко назовем jik
- первый цикл по j, второй по k, третий по i - кратко назовем jki
- первый цикл по k, второй по i, третий по j - кратко назовем kij
- первый цикл по k, второй по j, третий по i - кратко назовем kji
Пример цикла перемножения:
for (i=0;i<N;i++) for (j=0;j<N;j++) for (k=0;k<N;k++) testee[i][j] += A[i][k]+B[k][j];
Во всех 6 случаях решение задачи дает один и тот же результат, но совершенно разную производительность.
-fast ijk ikj jik jki kij kji Умножение матриц (сек.) 7.15 2.16 5.35 12.48 2.64 12.28 Ннаилучшую производительность показывает выбор варианта ikj, в случае выделения памяти под матрицы по строкам. Рассмотрим почему так получается:
for (i=0;i<N;i++) for (k=0;k<N;k++) for (j=0;j<N;j++) testee[i][j] += A[i][k]+B[k][j];
В случае ikj, в самом внутреннем цикле по j и по матрице B, и по результирующей матрице идет обход элементов в цикле по строке (а так как память выделяется по строкам, то обращение к соседнему элементу по строке происходит намного быстрее, чем обращение к соседнему элементу по столбцу). Логично предположить, что наиболее быстро будет выполняться перемножение матриц с организацией внутреннего цикла по j. Так и есть, лучшие варианты это ikj и kij. Ну а ikj оказался быстрее чем kij, так как во втором цикле по вложенности, в случае выбора цикла по k, пробегается матрица А по строке и матрица В по столбцу. В случае выбора цикла по I, пробегается две матрицы по столбцам (A и testee).
Таким образом, в данном примере, выбор грамотной организации вычислений, используя знания о размещении данных в памяти, дает выигрыш в 6 раз по сравнению с наихудшим выбором организации вычислений.
При решении задачи только сочетание правильного использования флагов оптимизации и правильной организации вычислений дает оптимальный результат.
Рассмотрим другую задачу, решение уравнения Пуассона, с теми же самыми флагами:
flags -O0 -O1 -O2 -O3 -fast Решение уравнения Пуассона (сек.) 19.98 9.04 6.99 6.9 6.51
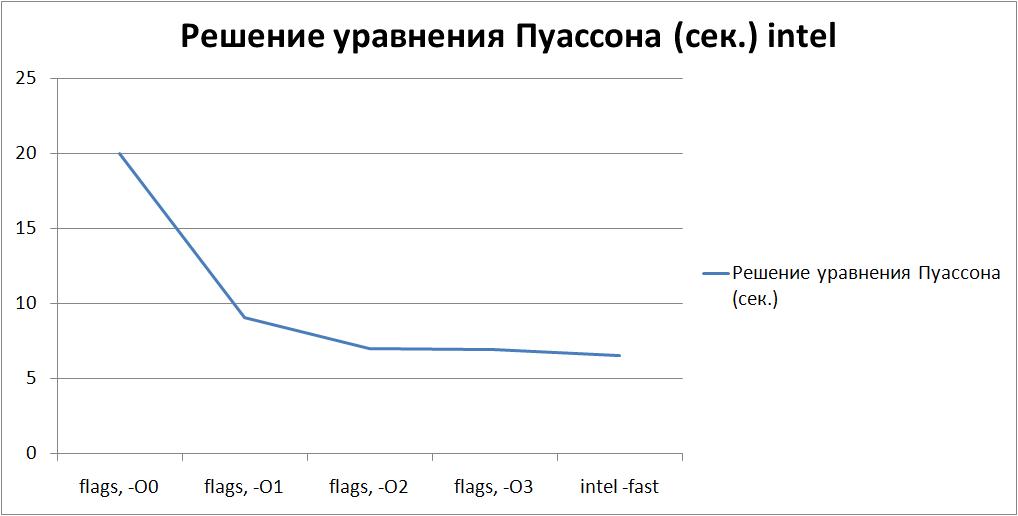
Здесь применение более агрессивной оптимизации дает выигрыш по времени порядка 7%.
Использование опций оптимизации компилятора дает существенный выигрыш в производительности, но не всегда более агрессивная оптимизация даст лучший результат. Во многих случаях достаточно базовой оптимизации -O2. Для компилирования программ на кластере СКИФ МГУ для начала следует попробовать опцию -O2, а уже затем пытаться использовать более агрессивную оптимизацию. Для получения базовой информации об оптимизации по компилятору Intel можно набрать icc -help opt в коммандной строке при входе на кластер. Для получения расширенной информации об опциях оптимизации можно набрать icc -help advanced либо обратиться к документации.
