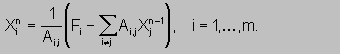| 1 | MAIN PART Jackoby. |
| 2 | BEGIN |
| 3 | Matrix: (Oi: (i=1..m); Oj: (j=1..m)). |
| 4 | Oj1, Oj2: Oj/j<>i. |
| 5 | VARIABLE X0, X, F DEFINED ON Oi. |
| 6 | VARIABLE A DEFINED ON Matrix. |
| 7 | VARIABLE Epsilon. |
| 8 | DOMAIN PARAMETERS m=4. |
| 9 | INPUT X0(FILE='jackoby') ON Oi. |
| 10 | INPUT F(FILE='jackoby') ON Oi. |
| 11 | INPUT A(FILE='jackoby') ON Matrix. |
| 12 | INPUT Epsilon(FILE='jackoby'). |
| 13 | OUTPUT X(FILE='jackoby.out') ON Oi. |
| 14 | ITERATION X ON n. |
| 15 | INITIAL n=0: |
| 16 | FOR Oi ASSUME X=X0. |
| 17 | END INITIAL |
| 18 | FOR Oi ASSUME X=1/A[j=i]*(F-SUM((Oj1)A*X[i=j,n-1])). |
| 19 | EXIT WHEN MAX((Oi)ABS(X[n]-X[n-1]))<Epsilon. |
| 20 | END ITERATION n. |
| 21 | END PART. |
Рассмотрим эту программу более подробно (используемые ниже номера совпадают с нумерацией строк программы).
(1) Заголовок главного раздела программы Jackoby.
(2) Начало главного раздела.
(3) Определяются многомерная область Matrix
(4) Определяются условные области Oj1, Oj2. Следует отметить, что эти области строятся путем наложения условия j<>i на область Oj, которая в своем описании имеет только индекс j. Как уже было сказано в разделе Описание условной области индексы величин, используемых при записи условия на индексы, не обязательно должны входить в множество индексов модифицируемой области, на которую накладываются условия - это могут быть внешние индексы. В нашем случае внешнем индексом является индекс i.
(5-7) Описание переменных X0 - начальное приближение, A - матрица коэффициентов системы, F - столбец свободных членов, Epsilon - погрешность вычислений, X - результат решения системы.
(8) Задание параметров областей (размерность матрицы).
(9-12) Ввод начальных данных X0, F, A и Epsilon из файла jackoby.dat, содержащего следующие строки:
X0(i=1..4)= 0.0, 0.0, 0.0, 0.0;
F(i=1..4)= 1.5471, 1.6471, 1.7471, 1.8471;
A(i=1..4,j=1..4)= 1.1161, 0.1254, 0.1397, 0.1490,
0.1582, 1.1675, 0.1768, 0.1871,
0.1968, 0.2071, 1.2168, 0.2271,
0.2368, 0.2471, 0.2568, 1.2671;
Epsilon = 0.0001;(13) Вывод результата в файл jackoby.out
(14-20) Конструкция итерации.
(18) Вычисление значения величины X по формуле
Область Oi, по которой ведется расчет содержит только индекс i. Запись A[j=i] означает, что берется элемент A(i,i) матрицы A; F - элемент F(i) столбца свободных членов F. Запись SUM((Oj1)A*X[i=j,n-1])) осуществляет вызов функции редукции SUM на условной области Oj1 при этом индекс j является внутренним, а i внешним индексом.
(21) Конец главного раздела.