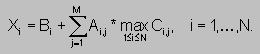Обращение к функциям в языке Норма
В языке определены:
Стандартные арифметические функции
К стандартным арифметическим функциям относятся функции:
SIN COS EXP SQRT ASIN ABS ALOG ALOG10 ENTIER ATAN
К функциям редукции относятся функции SUM(сумма), MULT(произведение), MAX(максимум), MIN(минимум).
Обращение к этим функциям имеет вид:
имя функции((имя области) арифметическое выражение).
Область определяет множество точек области, в которых необходимо вычислить функцию, арифметическое выражение - множество значений, к которым применяется функция. Пусть требуется вычислить
Фрагмент этого вычисления на языке Норма:
VARIABLE A, C DEFINED ON Oij: (Oi: (i=1..N); Oj: (j=1..M)).
VARIABLE B, X DEFINED ON Oi.
FOR Oi ASSUME X=B+SUM((Oj)A*MAX((Oi)C)).Для редукционных функций справедливо правило локализации индексов: область, указанная в качестве аргумента функции редукции, вводит свою систему индексов, область действия которой - арифметическое выражение, заданное в качестве второго аргумента функции редукции. Это означает, что индексы, используемые в арифметическом выражении, можно разделить на два типа: внутренние, то есть совпадающие с индексами области редукции и определяемые ими, и внешние, то есть не совпадающие с индексами области редукции, и определяемые внешними областями (например, областями других функций редукции или оператора ASSUME).
Множество значений внутренних индексов полностью определяется областью, заданной в качестве аргумента функции редукции. Множество значений внешних индексов определяется внешними по отношению к функции редукции областями.
Если внешняя область условная, то условие действует на все внешние индексы арифметического выражения, стоящего под знаком функции редукции.
Внешняя функция описывается пользователем. Обращение к ней представляется именем функции, за которым в круглых скобках следует список фактических параметров, разделенных запятыми. Результат вычисления функции представляется именем функции. Вычисление возможно, если все фактические параметры приняли соответствующие значения - все фактические параметры рассматриваются как исходные данные для вычисления функции, побочный эффект запрещен.
Фактическими параметрами внешней функции могут быть арифметические выражения, имена внешних разделов и внешних функций, либо величины на областях. Пример описания функции BOUND из примера Parabol:
FUNCTION BOUND DOUBLE.
k1,k2
BEGIN
VARIABLE k1,k2 DOUBLE.
VARIABLE pi DOUBLE.
pi=3.1415.
BOUND=SIN(pi*k1/k2).
END PART.и ее вызова:
FOR Wxt/j=0 ASSUME u=BOUND(i,M).
Оператор ASSUME задает правила вычисления вектора u(i,0), i=1,...,M, при этом для каждого i необходимо вычислить значение функции пользователя BOUND.
Число формальных и фактических параметров должно быть одинаковым (соответствие устанавливается слева направо в порядке написания).
Если и формальный, и фактический параметры являются величинами на областях, то должны совпадать число индексов областей и число точек в диапазонах по соответствующим индексам.