© Воеводин Вл.В.
Варианты заданий на использование MPI.
Воеводин В.В., Воеводин Вл.В.
Задание 1.
Имеется вычислительная система, состоящая из ![]() процессоров, каждый из
которых имеет быструю память величиной
процессоров, каждый из
которых имеет быструю память величиной ![]() для хранения обрабатываемых
данных и результатов. Известно, что время выполнения одной арифметической
операции
для хранения обрабатываемых
данных и результатов. Известно, что время выполнения одной арифметической
операции ![]() , намного меньше, чем время передачи одного числа
от процессора к процессору. Известно также, что выгоднее по времени
передавать большие пакеты данных, причем чем больше пакет, тем лучше.
, намного меньше, чем время передачи одного числа
от процессора к процессору. Известно также, что выгоднее по времени
передавать большие пакеты данных, причем чем больше пакет, тем лучше.
- Составить программу решения систем линейных алгебраических уравнений с
квадратной невырожденной матрицей порядка
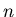 методом Гаусса (любой
вариант метода) с использованием языков Си и MPI.
методом Гаусса (любой
вариант метода) с использованием языков Си и MPI.
- Провести испытание программы на системе
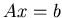 , где
, где
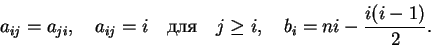
Решение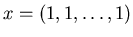 .
.
- Найти эксперементально зависимость времени
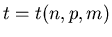 решения системы
как функции параметров
решения системы
как функции параметров 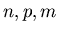 и вычислить коэффициенты потерь
и вычислить коэффициенты потерь
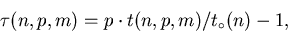
где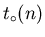 есть время, необходимое только для выполнения
арифметических операций при решении системы порядка
есть время, необходимое только для выполнения
арифметических операций при решении системы порядка 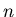 на одном процессоре.
на одном процессоре.
- Добиться того, чтобы при заданном
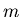 программа решала систему
максимально возможного (по главному члену) порядка.
программа решала систему
максимально возможного (по главному члену) порядка.
Литература
- В.А. Ильин, Г.Д. Ким. Линейная алгебра и аналитическая геометрия. М:,Изд-во МГУ, 1998, стр.13,101.
- В.В. Воеводин. Вычислительные основы линейной алгебры. М:,Наука, 1977, стр.293-295.
Задание 2. Перемножение квадратных матриц порядка ![]() любым способом
любым способом
Тест: любой
Литература
- В.А. Ильин, Г.Д. Ким. Линейная алгебра и аналитическая геометрия. М:, Изд-во МГУ, 1998, стр. 13,15.
- В.В. Воеводин. Вычислительные основы линейной алгебры. М:, Наука, 1977,стр.293-295.
Задание 3. Обращение матриц методом Жордана
Тест: матрица ![]() из системы уравнений
из системы уравнений
матрица ![]() :
:
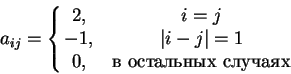
Литература
- В.А. Ильин, Г.Д. Ким. Линейная алгебра и аналитическая геометрия. М:, Изд-во МГУ, 1998, стр. 13,32-35.
- В.В. Воеводин. Численные методы алгебры (теория и алгоритмы). М:, Наука, 1966, стр. 64-67, 106-110.
Задание 4. Написать параллельную программу поиска всех решений задачи размещения N ферзей на шахматной доске K*K. Решением считается такое размещение, при котором ферзи не бьют друг друга.
Входные параметры программы:
- P - число параллельных процессов;
- N - количество ферзей;
- K - размер доски.
Замечание. Хорошая параллельная программа подразумевает, что, по возможности, выполняются следующие условия:
- Работа в параллельных процессах не дублируется.
- Вычислительная нагрузка на каждый процесс примерно одинакова.
- При увеличении числа процессоров в n раз (и соответствующем увеличении числа процессов), время решении задачи уменьшается, в идеальном случае, в n раз.
| Поддержка в Интернет: |
|
лаборатория Параллельных информационных технологий НИВЦ МГУ
|
