Задача суммирования элементов массива

Вводные замечания

Неискушённый в параллельном программировании читатель может быть удивлён тем, насколько простая задача выбрана для разбора.

Однако, во-первых, уже те студенты, что изучали математические основы распараллеливания на самом простом уровне, знают, что задача суммирования элементов массива является прекрасной моделью для распространения приёмов, используемых на ней, на другие, более сложные задачи. Ассоциативность операции скалярного сложения, позволяющая нам при конструировании алгоритма суммирования использовать различный порядок для получения ускорения, является общим свойством также и многих других операций (скалярного умножения, матричных сложения и умножения), что позволяет распараллеливать, казалось бы, такие нераспараллеливаемые последовательные методы, как схемы Горнера и прогонки. Поэтому если мы научимся эффективно суммировать массивы, то этим также сделаем большой шаг к эффективной реализации на этой вычислительной архитектуре и более сложных методов.

Во-вторых, не надо забывать о том, что специфические для различных архитектур задачи, возникающие при адаптации программ к этой архитектуре, удобнее всего рассмотреть именно на примере простых программ. А даже для простой программы важно прежде всего знать её теоретические основы.

Математика задачи и общеизвестные варианты её решения

Суммирование элементов прямоугольного массива допускает много вариантов решения, что связано с ассоциативностью основной элементарной операции (суммирования двух элементов) в идеальном исчислении. В реальном исчислении (на устройствах с ограниченной мантиссой в числах вещественного типа), естественно, ассоциативности нет, и анализ влияния ошибок округления должен проводиться для каждого варианта в отдельности.

Последовательный вариант

В этом варианте для накопления суммы используется один-единственный дополнительный вещественный элемент. На Фортране 77 соответствующая подпрограмма-функция будет выглядеть так:

       real function SEQSUM(A,N,M)
       real A(N,M), S
       S = 0.
       Do 10 I = 1,N
             Do 10 J = 1,M
                    S = S + A(I,J)
10    continue
        SEQSUM=S
        return
        end

При этом даже здесь есть возможность в представленном тексте, который реализует последовательное суммирование по строкам (см. схему алгоритма ниже, синим показаны элементарные сложения),

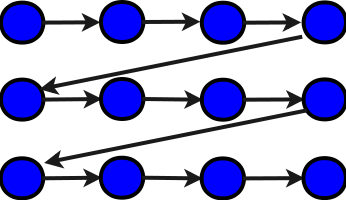
переставить местами циклы и получить последовательное суммирование по столбцам:

       real function SEQSUM(A,N,M)
       real A(N,M), S
       S = 0.
       Do 10 J = 1,M
             Do 10 I = 1,N
                    S = S + A(I,J)
10    continue
        SEQSUM=S
        return
        end

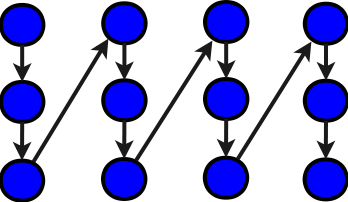
Ясно, что в обоих случаях ни о каком параллелизме речи быть не может. Критический путь 1 графа будет равен NM+1 (на графе не показано первоначальное присвоение нуля переменной S).

Вариант с разбиением суммирований по столбцам, последовательно-иерархический

В этом варианте для каждого из столбцов сумма накапливается отдельно, а потом эти полученные частные суммы прибавляются к общему "накопителю". На Фортране 77 соответствующая подпрограмма-функция будет выглядеть так:

       real function COLSUM(A,N,M)
       real A(N,M), S, R
       S = 0.
       Do 20 J = 1,M
             R = 0.
             Do 10 I = 1,N
                    R = R + A(I,J)
10          continue
              S = S+R
20    continue
        COLSUM=S
        return
        end

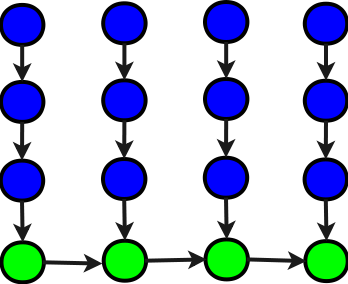
И синими, и зелёными обозначены элементарные операции сложения чисел. В даном графе алгоритма, как и ранее, мы опустили передачи начальных данных и инициализации временных переменных. Как видно, общее количество элементарных операций увеличилось на M, но при этом критический путь 1 графа уменьшился до N+M+2, так что вполне возможны параллельные реализации. Например, можно реализовать параллельно внутренний цикл в представленной функции. Не следует, однако, забывать, что тогда мало будет одной накопительной переменной R на все циклы, и надо будет её размножить в массив.

Пирамиды и каскадные схемы

Последовательные ветви (как в двух полностью последовательных вариантах, так и в последовательно-иерархическом) могут быть заменены на пирамиду. Наибольшую быстроту при таком распараллеливании даёт пирамида сдваиванием. Её, однако, редко записывают на последовательных языках, поскольку применяется-то сдваивание для распараллеливания.Если всё же записывают, то чаще с помощью рекурсивных вызовов, что не очень удобно для анализа графа. Причина - в том, что промежуточные результаты при нерекурсивной реализации надо хранить, и для этого нуже массив всего вдвое меньший, чем суммируемый. Рассмотрим подпрограмму пирамидного суммирования одномерного массива на Фортране 77 (простенький вариант для N, являющегося степенью двойки):

       real function PIRSUM(A,B,N, L)
C    L=logN
       real A(N), B(N/2)
       do 10 I=1,N/2
            B(I) = A(2*I-1)+A(2*I)
10    continue
       do 20 J = 1, L-1
            do 20 I=1,N/2,2**J
             B(I)=B(I)+B(I+2**(J-1))
20    continue
        PIRSUM=B(1)
        return
        end

Дадим её схему для суммирования 8 элементов на рисунке:

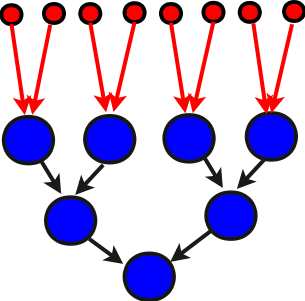
Здесь, как и ранее, синим цветом обозначены элементарные сложения, а чёрными стрелками - дуги графа алгоритма. Красным обозначены начальные данные (элементы массива) и их передача соответствующим вершинам графа алгоритма. Что хорошо в пирамиде сдваивания, это то, что в ней нет лишних элементарных сложений, и при этом имено она даёт минимальный критический путь 1 графа алгоритма.

Теперь рассмотрим рекурсивный вариант программы (на Си), но уже для произвольного N:

double PIRSUM(a,N)
double *a;
int N;
{
double s; int i,j;
 if (N<=0) {
  s=0.;
  return s;
 }else if (N==1) {
  s=*a;
  return s;
 }else{
  i=N/2; j=N-i;
  s=PIRSUM(a,i)+PIRSUM(a+i,j);
  return s;
 }
}

Её схема при равных N аналогична схеме предыдущей подпрограммы. Однако, при использовании такой схемы для гигантских N рекурсия всё же нежелательна, поскольку при большой глубине вызовов подпрограмм может переполниться стек, который часто используют для хранения параметров вызова во многих трансляторах.

Сложные каскадные схемы суммирования прямоугольного массива предполагают замену такой вот пирамидой последовательных участков (как синих, так и зелёных) предыдущей иерархически-последовательной схемы.

1Критическим путём в ациклическом ориентированном графе (коим является граф алгоритма) называется самый длинный из путей. Здесь мы считаем его по количеству вершин на пути.

Ошибки округления при суммировании

Мы видели в предыдущем разделе, что даже для такой, на первый взгляд, простой математической операции может быть очень много разных реализаций. Следует, однако, помнить, что такое многообразие схем объясняется использованием ассоциативности операции сложения. Это свойство, однако, не является справедливым для машинных реальных операций сложения. Из-за этого при использовании разных алгоритмов суммирования у использующего получатся разные ошибки округления. Этот факт необходимо помнить, особенно когда такие суммирования используются внутри других алгоритмов как малые составные части, поскольку разный порядок совершения операций может стать причиной неустойчивости, если был реструктурирован даже изначально устойчивый алгоритм.

Если суммирование является самостоятельной частью алгоритма, а не входит существенным образом в другие операции (например, векторные, матричные), то с точки зрения минимизации ошибок округления в среднем выгоднее применять пирамидальное суммирование сдваиванием. Это, однако, никак не сказывается на теоретических оценках максимума ошибок результата - для каждого вида суммирования можно найти такое распределение, которое будет получать наибольшую ошибку именно для этого вида.

Реализация суммирования на некоторых параллельных вычислительных системах

Помимо общих слов о том, что ряд библиотек пакетов, предназначенных для параллельной реализации, содержит специальные подпрограммы суммирования, остановимся на двух примерах реализаций: под средой MPI, предназначенной для кластерной архитектуры, и на языке Colamo (для ПЛИСов). Упомянем только, что суммирование не очень хорошо ложится на конвейерную архитектуру, на которой, пожалуй, самой быстрой будет векторная реализация иерархически-последовательных схем.

Реализация под средой MPI

Программирующие в среде обмена сообщениями MPI, конечно, могут использовать вышеприведённые схемы суммирования массива, распределённого по секциям памяти разных узлов кластера, самостоятельно, с помощью подпрограмм пересылки сообщений. Однако сами такие сообщения окажутся (для любой из выбранных схем) очень короткими, что при недостаточном опыте программиста отрицательно скажется на производительности системы. Поэтому разработчики среды предусмотрели выполнение массовых операций с помощью специальных подпрограмм, в которых уже заложены пересылки, не самым худшим образом оптимизированные под среду. Это - две подпрограммы: MPI_Allreduce и MPI_Reduce. Различаются они только тем, что во второй подпрограмме результат получает только один из узлов MPI, а не все (как в первой). Что показательно, подпрограммы эти могут выполнять не только суммирование массива, но и три других массовых операции по всему массиву: вычисление минимума, максимума и произведения. Для тех читателей, что заинтересовались данной страницей о суммировании в связи с универсальностью его вычислительных схем, данная новость обладает двойственным характером. С одной стороны, для описанных простых операций это хорошо, и неопытные в MPI программисты могут пользоваться ими. Однако то, что в списке базовых операций для этих подпрограмм отсутствуют более сложные (скалярное произведение, матричное умножение и т.п.), означает, что для этих операций надо будет писать реализации описанных выше схем с помощью ручного программирования и программ пересылки сообщений. Что, однако, будет в отношении замедления производительности (как, впрочем, и для описанных четырёх операций) уже не таким критичным, поскольку при выполнении более сложных операций матричного типа длина сообщений существенно увеличится, а главное - увеличится ещё больше доля "арифметики" между межузловыми обменами данных.

Но главное - то, что даже в отношении указанных 4 операций (*, +, max, min) опытные программисты под MPI с помощью умелого группирования выполняют масовые суммирования (умножения и др.) без использования этих двух подпрограмм не медленнее, а даже несколько быстрее, чем с их использованием.

Реализация на ПЛИСах

При реализации на языке Коламо для ПЛИСов важен такой вопрос, как планирование ресурсов, которые будут отведены на реализацию задачи. В качестве примера приведём программу, реализующую пирамидально-конвейерную схему с использованием 16 сумматоров:

Program Piramida_Summatorov;
include MyLibNewElement;

VAR a : array real [16:vector, 100:stream] mem;
VAR res : real mem;
VAR i, j, k, l, m, n, s, kk, vect, vectd2 : number;
VAR cm1, cm2, cm3, cm4, cm5, cm6 : real com;
VAR c : array real [8:vector, 8:vector] com;
VAR rg : real reg;

Define vect=16;
Define vectd2=7;//vect/2-1
Define n=100;
Define m=3;
Define k=0;
Define kk=0;
Define l=8;//vect/2

Cadr ev;
for s:=0 to n-1 do
begin
    for i:=0 to vectd2 do
    begin
        c[0,i]:=a[k,s]+a[k+1,s];
        k:=k+2;
    end;
    for j:=1 to m do
    begin
        kk:=0;
        l:=l/2;
        for i:=0 to l-1 do
        begin
            c[j,i]:=c[j-1,kk]+c[j-1,kk+1];
            kk:=kk+2;
        end;
    end;
    rg:=rg+c[m,vectd2];
end;
res:=rg;
EndCadr;
End_Program.

Эта программа реализует каскадно-пирамидальную схему с использованием конвейеризации. Более детально вопросы программирования на Коламо при применении различных схем суммирования (по материалам семинара НИИ МВС при ТРТУ) будут рассмотрены в отдельном месте.

Заключение

Итак, мы видим, что даже для простейших задач разных алгоритмических реализаций может быть уйма. Это, собственно, и объясняет то, что ими продолжают и продолжают заниматься исследователи, особенно когда приходится адаптировать задачу на новой вычислительной архитектуре и потому выбирать из множества реализаций ту, что лучше всех подойдёт для отображения на эту архитектуру.

© Лаборатория Параллельных информационных технологий НИВЦ МГУ
Rambler's Top100