Рассмотрение различных приёмов программирования на Colamo на примере решения задачи суммирования элементов массива

На примере программирования задачи суммирования элементов массива разберём некоторые приёмы программирования на языке Colamo.

Вводные замечания

Неискушённый в параллельном программировании читатель может быть удивлён тем, насколько простая задача выбрана для рассмотрения приёмов программирования на языке Colamo. Однако, во-первых, уже те студенты, что изучали математические основы распараллеливания на самом простом уровне, знают, что задача суммирования элементов массива является прекрасной моделью для распространения приёмов, используемых на ней, на другие, более сложные задачи. Ассоциативность операции скалярного сложения, позволяющая нам при конструировании алгоритма суммирования использовать различный порядок для получения ускорения, является общим свойством также и многих других операций (скалярного умножения, матричных сложения и умножения), что позволяет распараллеливать, казалось бы, такие нераспараллеливаемые последовательные методы, как схемы Горнера и прогонки.Поэтому если мы научимся эффективно суммировать на ПЛИСах массивы, программируя на Colamo, то этим также сделаем большой шаг к эффективной реализации на этой вычислительной архитектуре и более сложных методов.

Во-вторых, не надо забывать о том, что специфические для ПЛИС задачи, возникающие при адаптации программ к этой архитектуре, удобнее всего рассмотреть именно на примере простых программ. В данном случае важной проблемой будет не столько распараллеливание суммирования массива, сколько фиксация ресурсов вычислительной системы, отводимой под конкретную часть вычислительной задачи. Рассмотрение будет начато несколько "издалека", с неудачных примеров, с постепенным подходом к решению поставленной задачи. Данный подход объясняется тем, что типичные ошибки в Коламо несколько другие, чем в обычных языках высокого уровня.

Постановка задачи

Рассмотрим решение задачи последовательного суммирования элементов массива NxM. Ресурс сумматоров фиксированный - 8 штук. Обращаем внимание читателя на ограниченность количества сумматоров. Как уже говорилось во вводных замечаниях к настоящему тексту, место сумматора, если мы будем рассматривать более сложные алгоритмы, может занять реализация более сложной операции (скалярной, матричной и т.п.) Поэтому читателя, знающего реальные ресурсы на ныне выпускаемых ПЛИСах, не должна удивлять кажущаяся малость цифры 8. Она может быть связана как с модельностью рассмотрения, так и с другими причинами вроде включения данной задачи в качестве составляющей более сложного алгоритма.

Математика задачи и общеизвестные варианты её решения

Суммирование элементов прямоугольного массива допускает много вариантов решения, что связано с ассоциативностью основной элементарной операции (суммирования двух элементов) в идеальном исчислении. В реальном исчислении (на устройствах с ограниченной мантиссой в числах вещественного типа), естественно, ассоциативности нет, и анализ влияния ошибок округления должен проводиться для каждого варианта в отдельности.

Последовательный вариант.

В этом варианте для накопления суммы используется один-единственный дополнительный вещественный элемент. На Фортране 77 соответствующая подпрограмма-функция будет выглядеть так:
       real function SEQSUM(A,N,M)
       real A(N,M), S
       S = 0.
       Do 10 I = 1,N
             Do 10 J = 1,M
                    S = S + A(I,J)
10    continue
        SEQSUM=S
        return
        end

При этом даже здесь есть возможность в представленном тексте, который реализует последовательное суммирование по строкам (см. схему алгоритма ниже, синим показаны элементарные сложения),

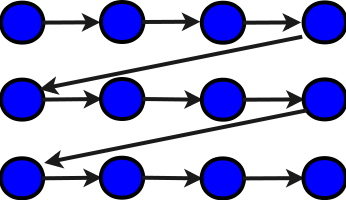
переставить местами циклы и получить последовательное суммирование по столбцам:

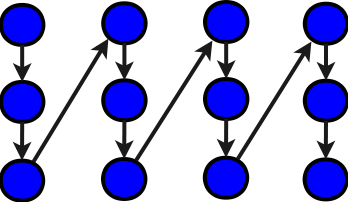
Ясно, что в обоих случаях ни о каком параллелизме речи быть не может. Критический путь¹ графа будет равен NM+1 (на графе не показано первоначальное присвоение нуля переменной S).

Вариант с разбиением суммирований по столбцам, последовательно-иерархический

В этом варианте для каждого из столбцов сумма накапливается отдельно, а потом эти полученные частные суммы прибавляются к общему "накопителю". На Фортране 77 соответствующая подпрограмма-функция будет выглядеть так:

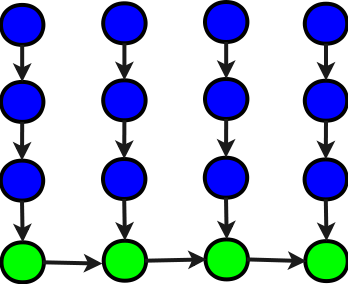
И синими, и зелёными обозначены элементарные операции сложения чисел. В даном графе алгоритма, как и ранее, мы опустили передачи начальных данных и инициализации временных переменных. Как видно, общее количество элементарных операций увеличилось на M, но при этом критический путь¹ графа уменьшился до N+M+2, так что вполне возможны параллельные реализации. Например, можно реализовать параллельно внутренний цикл в представленной функции. Не следует, однако, забывать, что тогда мало будет одной накопительной переменной R на все циклы, и надо будет её размножить в массив.

Пирамиды и каскадные схемы

Последовательные ветви (как в двух полностью последовательных вариантах, так и в последовательно-иерархическом) могут быть заменены на пирамиду. Наибольшую быстроту при таком распараллеливании даёт пирамида сдваиванием. Её, однако, редко записывают на последовательных языках, а если записывают, то с помощью рекурсивных вызовов, что не очень удобно для анализа графа. Здесь мы только дадим её схему для суммирования 8 элементов на рисунке:

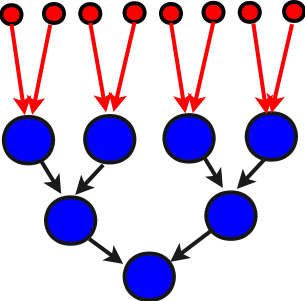
Здесь, как и ранее, синим цветом обозначены элементарные сложения, а чёрными стрелками - дуги графа алгоритма. Красным обозначены начальные данные (элементы массива) и их передача соответствующим вершинам графа алгоритма. Что хорошо в пирамиде сдваивания, это то, что в ней нет лишних элементарных сложений, и при этом имено она даёт минимальный критический путь¹ графа алгоритма. Сложные каскадные схемы суммирования прямоугольного массива предполагают замену такой вот пирамидой последовательные участки (как синие, так и зелёные) предыдущей иерархически-последовательной схемы.

¹Критическим путём в ациклическом ориентированном графе (коим является граф алгоритма) называется самый длинный из путей. Здесь мы считаем его по количеству вершин на пути.

Структура, получающаяся при использовании одной накапливающей переменной

Теперь рассмотрим не граф алгоритма, а вычислительную структуру², в соответствии с которой реализовано последовательное суммирование, использующее одну накапливающую переменную, но все восемь сумматоров:

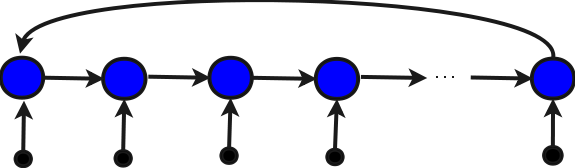
Структура представляет собой группу из восьми сумматоров, соединенных последовательно, что само по себе уже показывает плохое параллельное программирование в фрагменте. Каждый сумматор структуры последовательно подсуммирует определенные элементы вектора. Очевидно, что на эту структуру нельзя подавать элементы до тех пор, пока не будет выполнено суммирование на последнем, восьмом сумматоре, и не придет результат по обратной связи. В результате этого структура будет большую часть времени простаивать. Суммирование с помощью такой структуры будет медленнее, чем обычное суммирование на одном процессоре. Поэтому при создании структуры необходимо минимизировать длину обратной связи.

Правильная структура организации суммирования

Рассмотрим более правильную вычислительную структуру²:

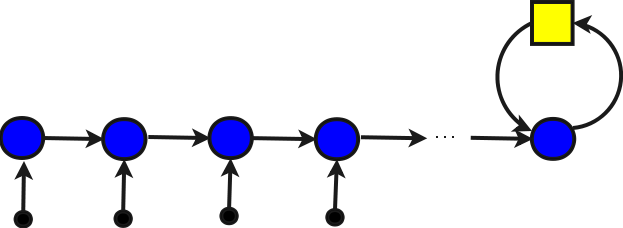
Данная структура во многом похожа на предыдущую. Здесь также используются 8 сумматоров, но последний сумматор имеет обратную связь, на которой стоит регистр. Этот сумматор выполняет подсуммирование результатов. Главное отличие данной структуры от предыдущей в том, что на эту структуру элементы массива могут подаваться по мере их поступления. Результат задерживается только на одном, последнем сумматоре, а суммирование на всех остальных сумматорах выполняется аналогично предыдущей структуре. Если бы задержка на сумматоре составляла 1 такт, то структура работала бы в потоке. В дальнейшем будут рассмотрены способы, которые позволят обеспечить плотный поток для таких структур. В отличие от предыдущей, данная структура работает в 8 раз быстрее, поскольку не простаивает.

Заметим также, что порядок суммирования в ветви, подающей результат на последний сумматор, не так важен - лишь бы не было петель. Поэтому в качестве подающих ветвей могут быть рассмотрены разные структуры². Их мы сейчас и рассмотрим, а записаны они будут на Colamo..

²Под структурой здесь везде понимается набор вычислительных ресурсов (в данном случае сумматоров) ПЛИС, со связями между ними. Она не имеет ничего общего со структурами данных в обычных языках (типа Си, Паскаля и т.п.)

Пирамида сумматоров (сдваивание)

Теперь рассмотрим суммирование элементов массива с помощью пирамиды сумматоров.

EndSubCadr;

Результат суммирования out_com, получаемый после выполнения подкадра на каждой итерации цикла, подсуммируется со значением, которое содержится в регистровой переменной sum.

Знакомые с приёмом сдваивания, наверное, сразу заметили, что хоть сумматоров и 7, но используются они не одновременно, а (при прохождении по пирамиде сдваивания) сначала 4, потом 2, потом последний в пирамиде. Поэтому суммирование пирамидой само по себе в этом варианте не даст полной эффективности и должно использоваться с чем-то ещё.

Последовательное суммирование элементов массива

Рассмотрим следующий пример программы, реализующей последовательное суммирование элементов массива.

В кадре Sum1 организуется цикл по элементам потока. В теле цикла вызывается структура A, которая задана с помощью конструкции Let. В качестве входных параметров структура² A принимает элементы входного массива x, а так же переменную cm1. В качестве результата структура A возвращает модифицированную переменную cm1, которая сохраняется в мемориальной переменной summa.

Рассмотрим структуру A. Сначала выполняется инициализация регистровой переменной rg, которая необходима для подсуммирования результатов. В нее записывается входной параметр s, который в начальный момент времени равен нулю. Далее организуется цикл по переменной j до переменной chan_p, которая определяет количество порций каналов по 8. В данном случае таких порций две: в одной восемь каналов, в другой - два. В данном цикле организован цикл по переменной i до переменной chan_m, которая задана константой и равна 8. Это количество каналов в j-й порции. Если номер канала меньше 10, поскольку это общее количество каналов, то выполняется подсуммирование с предыдущим результатом.

При такой реализации каналы, номера которых превышают 10, не заполняются нулями и вместо значения канала выдается значение y1 на предыдущем шаге.

Использование пирамиды сумматоров

Рассмотрим пример программы, реализующей суммирование элементов массива с использованием пирамиды сумматоров.

Program Sum_piramidalno;
include MyLibNewElement;
VAR x : array real [10 : Vector, 20 : Stream] mem;
VAR summa : real mem;
VAR i, j, chan, chan_m, chan_p, n : number;
VAR cm1 : real com;
// переменные Let'а
VAR xl : array real [10 : Vector] com;
VAR res : real reg;
VAR s : real com;
Define chan=10;
Define chan_p=2; // 10/8+1
Define chan_m=8;
Define n=20;
Define summa=0;
CADR Sum1;

endlet;

В данной программе основной кадр Sum1 полностью аналогичен тому, который использовался в предыдущем примере. Рассмотрим структуру A, которая реализует суммирование с помощью пирамиды сумматоров. Структура A во многом аналогична соответствующей структуре предыдущего примера. В то же время, цикл по переменной i в данном случае выполняется до значения chan_m/2. В теле цикла используются два оператора if, которые выполняют суммирование элементов в зависимости от их номеров в массиве. Далее организуется пирамида сумматоров и выполняется подсуммирование результата, полученного с пирамиды сумматоров, с предыдущим результатом. Результат накапливается в регистровой переменной rg.

Недостаток программы - в низком классе программирования. Это касается фрагмента кода, который реализует пирамиду сумматоров в структуре A. При использовании такого подхода программа реализации пирамиды, состоящей из нескольких сотен сумматоров, будет очень громоздкой.

И снова - последовательное суммирование элементов массива

Рассмотрим пример программы, реализующей последовательное суммирование элементов массива.

program Test_5;//Сумма последовательно

end_program.

Для данного примера найдено удачное решение: массив разделен на восемь. Сначала вычисляется результат для самого первого сумматора последовательности c[0], а дальше выполняется последовательное суммирование. Для накопления результата используется регистровая переменная sum. Стоит отметить, что в данной программе не используется оператор if. Программа компактная и легко читается. Вместе с тем в ней остались проблемы, связанные с фиксированным заданием первой размерности суммируемого массива.

Возвращаемся к пирамиде сумматоров

Рассмотрим пример программы, реализующей суммирование элементов массива с использованием пирамиды сумматоров.

program Test_4;//Сумма пирамидой

end_program.

Недостаток программы - в низком классе программирования. Такой подход (ручное, по сути, сдваивание) не годится для случая, когда пирамида состоит из множества сумматоров (порядка нескольких сотен).

Снова последовательные суммирования разного вида

Рассмотрим пример программы, реализующей последовательное суммирование элементов массива.

Program SimpleSumArray;

End_Program.

Здесь N и M - размерности массива, N1 и M1 - индексы для организации циклов. ResSum - мемориальная переменная для хранения результата суммирования. Sum - регистровая переменная для организации подсуммирования. Организованы два вложенных цикла: первый - по элементам потоков, второй - по элементам вектора. Структура вычислений в этом примере реализуется следующим образом: стоит один регистр, один сумматор, затем - мультиплексор, который выбирает нужные данные, поступление которых на вход мультиплексора регулируется с помощью задержек.

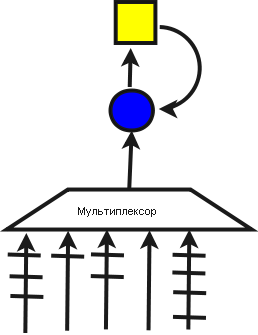
Рассмотрим еще один пример последовательного суммирования элементов массива.

Program SimpleSumArray;

End_Program.

Здесь программистом допущена ошибка. Нарушено правило единственной подстановки для переменной ComSum.

Комбинация пирамиды и последовательности

Теперь, после рассмотрения разных по стилю и не лишённых недостатков, а кое-где и ошибок, программ, посмотрим всё же, как реально ограничить использование ресурса (сумматоров), не фиксируя при этом размерности массива и при этом используя ресурс с максимальной эффективностью.

4 сумматора

Рассмотрим пример программы, реализующей последовательное и пирамидальное сложение с использованием 4-х сумматоров:

Здесь использован подкадр, в котором реализовано последовательное суммирование (закомментировано в программе), а также пирамида сумматоров. Оба варианта используют 4 сумматора. Однако возникает вопрос насчет естественного порядка при последовательном суммировании. Где гарантия, что будет соблюден естественный порядок? В данном случае лучше использовать скобки, которые жестко зададут естественный порядок суммирования элементов.

Далее приведен кадр для подачи данных в подкадр Sum4Vect, причем с возможностью масштабирования для любой размерности массива:

Такой пример был рассмотрен на семинаре. Мы же здесь, отметив, что выбор альтернативы в кадре происходит внутри двойного цикла, наверное, могли бы с позиции опыта программирования на традиционных языках высокого уровня посчитать, что более экономным (в отношении не сумматоров, а других элементов ПЛИС) будет другое написание кадра:

а для других архитектур могли бы ещё наэкономить, разбив внешний цикл на основную часть (делящуюся на 4) и остаток, в котором и сосредоточились бы все проверки условий. Однако будет ли подобная оптимизация действительно экономной для ПЛИС?

Оказывается, нет.
В приведенном первым фрагменте написано более правильно. Это связано с особенностью структурной реализации условного оператора: при структурной реализации оператора условного выбора if - then - else структурно реализуются обе ветки условия (и для then, и для else), а на выход выдается результат с мультиплексора, объединяющего результат вычислений, на управляющий вход которого подаётся результат вычисления условия if. Дополнительно к этому, все вычисления в теле кадра выполняются с максимально возможной степенью параллелизма, если между ними нет информационной зависимости. Поэтому для приведенного примера, где I - векторная компонента, а J - потоковая, произойдет распараллеливание внутреннего цикла, содержащего условие, по числу векторных компонент внешнего цикла (т.е. при N1 = 9 будет 3 внутренних цикла, каждый из которых содержит условие из 4 веток. Итого - циклов 3, условий 3, подкадр 1). В предлагаемом в качестве более экономной альтернативы втором варианте произойдет распараллеливание оператора условия, содержащего 4 цикла и вызовы структурной составляющей подкадра Sum4Vect, что приведет к существенному увеличению занимаемого аппаратного ресурса (при N1 = 9 будет 3 условия, каждое из которых содержит 4 цикла и 4 подкадра. Итого - циклов 12, условий 3, подкадров 12). Скорость выполнения обоих рассматриваемых вариантов одинакова, но второй вариант занимает вычислительный ресурс в 4 раза больше, чем первый и поэтому обладает меньшей эффективностью. При программировании на Colamo нельзя пользоваться общепринятыми для фон-неймановских архитектур критериями эффективности программы, поскольку в расчет кроме компактности записи и скорости реализации необходимо также принимать критерий используемого ресурса оборудования. Поэтому важно вовремя остановиться на скользком пути оптимизации в стиле последовательного программирования, когда имеешь дело с программированием для ПЛИСов.

8 сумматоров

Ниже приведен пример программы, реализующей последовательное и пирамидальное сложение с использованием 8-ми сумматоров:

Program SumArray_8Sum;

Как и в случае с пирамидой суммирования из 4 сумматоров, в данной программе на первый взгляд может показаться не вполне экономной организация заполнения данных для основного подкадра, но, как и в пирамиде для 4 сумматоров, это только кажется привыкшим к традиционному стилю программирования. Вместе с тем отметим, что эта проблема не настолько важна, как проблема универсальной настраиваемой масштабируемости по ресурсам, которые у нас будут в распоряжении. В этом плане, конечно, данная программа выглядит не так коряво, как уже рассмотренная выше, но по сути в ней осталась заложена немасштабируемость ресурсов. Хотя главной задачей для нас при рассмотрении примеров было понять, как вообще ограничиваются используемые в ПЛИС ресурсы при программировании, отметим, что проблема масштабируемости не так сложна, как кажется. Скажем, при программировании пирамиды на 16 сумматоров можно использовать такую программу (причём мы видим, что в ней число 16 вовсе не существенно - вместо него может быть параметр, равный как 1024, так и 2²⁰ и даже более):

Как ограничиваются ресурсы при программировании на Colamo

Рассмотрим задачу суммирования элементов массива, для решения которой имеется 4 сумматора и множество каналов распределенной памяти, например, 24, и при этом нет потока.

DCL A [ 24 : vector ]

Необходимо сложить элементы массива последовательно-параллельно, потому что есть некоторый подкадр, который суммирует эти элементы по четыре. Предположим, что существует некоторая функция Add, которая выполняет суммирование:

Add(R, R', a)
dcl R, R' : com;
dcl a : [4 : vector] com;
R':=R+a1+a2+a3+a4

Как нужно обратиться к подкадру Add, при условии, что входной параметр - вектор, а также чтобы не произошло размножение элементов add? Если написать:

R[0]:=0
For i:=1 to 5 do
Add (R[i-1], R[i], a[i*4-3]) ,

то здесь R - информационно-независимые коммутационные переменные, A - вектор. При организации цикла элементы распараллелятся, в результате чего потребуется 24 сумматора. Это произойдет, если приведенный выше фрагмент кода будет находиться в теле кадра:

R[0]:=0
cadr
for i:=1 to 5 do
add (R[i-1], R[i], a[i*4-3])
endcadr

Но если оператор цикла будет вынесен за пределы кадра, то тогда произойдет последовательное обращение:

R[0]:=0
for i:=1 to 5 do
begin
cadr
add (R[i-1], R[i], a[i*4-3])
endcadr
end;

Поэтому введение в программу, реализующую последовательное и пирамидальное сложение с использованием 8-ми сумматоров, переменной Stream18VectorArr, которая предотвратит распараллеливание, абсолютно оправдано.

Следует отметить, что не всегда можно вынести операторы цикла за пределы кадра, поскольку это приведет к тому, что смысл программы изменится. Поэтому единственный выход - делать переприсваивания элементов массива с использованием специально описанной для этого переменной. Необходимо помнить, что операция переприсваивания одних коммутационных переменных в другие коммутационные переменные не занимает ни ресурсы, ни время. Операция переприсваивания выполняется только транслятором и является своего рода указанием, как сформировать информационный граф.

Заключение

При подготовке данной страницы в качестве базы были использованы материалы семинара НИИ МВС ТРТУ по языку Colamo. Редактор страницы убрал лишние, с точки зрения задачи фиксирования ресурсов, "отходы в сторону" вроде того, где будут использованы эти суммирования, поскольку считает переход к реально сложным программам на этом этапе преждевременным, а также добавил в ряде мест комментарии, понятные программистам на других языках. В этом плане пока что структурные рисунки (в начале текста) столь обширно прокомментировать нельзя, ибо без привыкания к схемотехническому, до определённой степени, мышлению, эффективное программирование на Colamo не представляется возможным в принципе.

Обращаю внимание читателя, что здесь в текстах программ уже появляются некоторые расширения начального стандарта языка, в частности, например, include, в Коламо, в отличие от Си, подключающий структурные библиотеки элементарных операций и задание структуры. При этом надо чётко помнить, что в Colamo, в отличие от языков типа Си, задают не структуру данных, а структуру вычислений.

© Лаборатория Параллельных информационных технологий НИВЦ МГУ